ALI Research Staff | Published January 04, 2022
Let's explore computational or mathematical fluency, a key component of STEM education.
Math fluency is a combination of skills that enables pupils to solve mathematical problems with ease and confidence; it is fundamentally about more than merely crunching numbers.
The three fundamental components of math fluency are accuracy, flexibility, and efficiency.
Each of these three elements is essential to the development of math fluency in students.
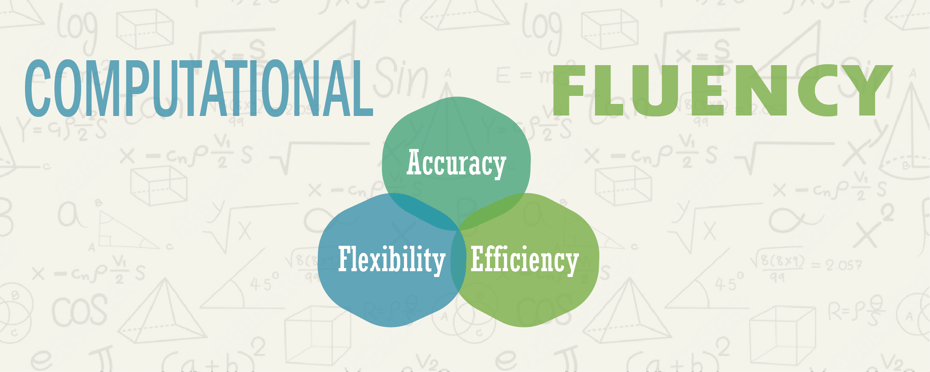
Getting the right answer is, of course, a logical and reasonable goal for students approaching a math problem.
In particular, as long as high-stakes assessments rely on simple multiple-choice format for most test items, this goal is the only one we’re measuring.
Without abandoning the target of accuracy, we can enhance students’ mathematical fluency and even, ultimately, their achievement in a testing environment if we ask even more of students than just producing right answers.
First of all, by emphasizing comprehension more, the anxiety caused by poor math performance can be reduced.
Errors are bound to happen.
If students focus only on the output, simple mistakes can easily discourage students, especially those in the early stages of mastering a new skill.
Students can quickly come to the conclusion that they aren’t good at math. If, however, teachers implement strategies for fluency in the mathematical process, they can gain the confidence that they “know what they’re doing” even if answers sometimes come out wrong.
Fostering a culture of sophisticated mathematical reasoning begins with encouraging students to explain their thought processes and solutions. This includes classroom techniques, such as Number Talks, that ask students to share their ideas to problem-solving with classmates.
When they explain their thinking, students not only improve computational fluency but also develop a better grasp of the underlying concepts.

The effects of the epidemic emphasize the importance of computational fluency in today's evolving educational environment.
Flexibility, which is crucial for adaptive problem-solving, is the foundation on which the development of innovative math instruction is built.
By allowing for multiple and individually relevant contexts and approaches, flexibility gives math life beyond rote memorization and enables students to apply principles in real-world situations.
Flexibility not only fuels creativity, it also promotes problem-solving. Innovative thinkers who take a non-traditional approach to problems are empowered when they develop a wider arsenal of strategies, encouraging creative exploration of mathematical methods.
Flexibility offers a ray of hope amid the gloom of learning loss.
By leveraging its power, teachers can help pupils bridge gaps quickly, hastening conceptual growth. Flexibility helps remote learning as well by allowing students to creatively acclimate to virtual environments and the new landscape of hybrid learning.
Rather than thinking of efficiency in computation as simply speed, we need to acknowledge its close relationship to flexibility.
Often, what most helps students arrive at effective solutions is being able to select the method they are most comfortable with and can implement most proficiently.
The insistence that all students acquire the same speed, always using the same method, can actually slow some students down and compound the ill effects of learning loss.
Students’ ability to choose the most efficient solution for them becomes essential when dealing with assessments that must be completed quickly.
A unique instructional fusion is achieved when flexibility and efficiency are paired.
By implementing instructional strategies for fluency that combine these elements, teachers develop flexible thinkers who are also equipped with the skills needed to solve mathematical problems precisely.
This seamless fusion turns mathematics from a mechanical task into a dynamic, strategic undertaking.
Of course, empowering students with the skills needed to select and implement the optimal strategies to solve math problems isn’t the whole story.
No matter how much skill a surgeon demonstrates during a challenging operation, the final evaluation rests with the outcome.
What was the outcome for the patient?
Similarly, we often reduce our assessment of students’ problem-solving skill by asking one simple question.
Did they get the correct answer?
Those of us in education who are paying attention understand the importance of computational fluency outside of the classroom as part of an essential lifelong skill set.
Mathematical proficiency isn’t just a prerequisite for many fields, including engineering, computer science, finance, and healthcare, but a way for students to analyze facts, make wise decisions, and solve practical problems they encounter every day.
As we look to the future, it's critical to acknowledge the essential role that educators have played in guiding this transition into a new era of math instruction.
Provided with the proper professional development and supported by a well-designed curriculum, they have the power to engage and inspire students as they gain computational fluency, creativity, and critical thinking.
Together we can bring about this mathematical revolution as we move forward and collaborate to empower students so they are ready for the opportunities and challenges of the future.

At the start of the school year, teachers have the chance to create a math classroom where every student feels valued...

Math manipulatives are a great way to make math more accessible for your students, especially if you know they may...

Storytelling is one of the oldest forms of communication as a way to share experiences, understand others, and...